Lattice paths
Lattice paths
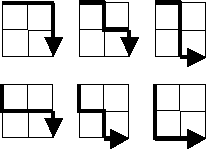
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
How many such routes are there through a 20×20 grid?
1.递推法
递推法:dp[x][y] = dp[x - 1][y] + dp[x][y - 1]
- 网格中到达任意一点的路径方案数 = 正上方方案数 + 正下方方案数:
dp[x][y] = dp[x - 1][y] + dp[x][y - 1] - 递推边界为左上角点(1,1),结果为右下角点坐标(4,4)
定义循环
(i, j)需要从点(1, 1)点开始这样外边界有一圈保护0,不需要判断边界、不用考虑数组越界问题(数字0不会影响答案)
1 |
|
2.组合问题
1 |
|
注意:如果是带有障碍物的问题则数学方法将不再适用,可以在方法1的基础上加入条件判断解决
3.有限制的路径方案数
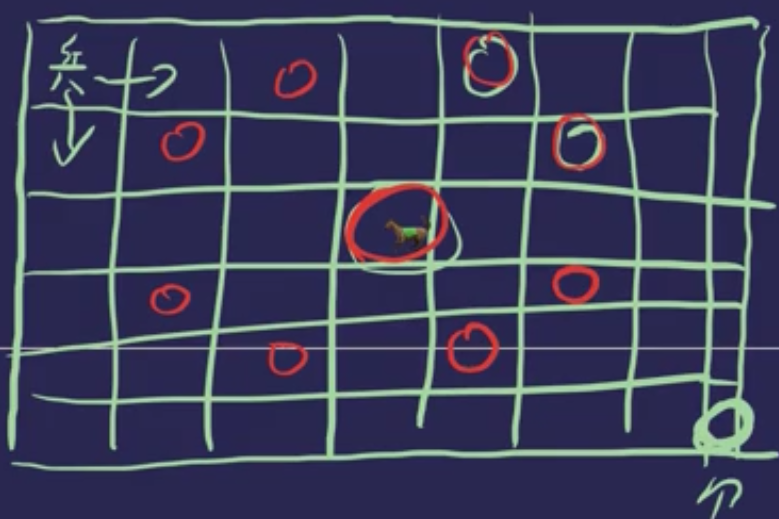
马踏过河问题
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.